探究导数在高中数学中的应用

摘 要

导数（Derivative）是微积分中的重要基础概念，是微积分计算的工具，由法国数学家费马（Fermat）所创。导数还是连接初等数学和高等数学的重要纽带，不仅有着广泛的应用，而且也为大学生进入高等学校学习高等数学奠定了基础。在高中数学中加入导数，给高中数学增添了新的活力，对于导数的学习，可以让学生更好的去了解函数形态，利用导数解决函数的最值、单调区间等问题。对于学生最难理解的函数图像问题，导数也提供了更好的研究方法，使学生能更加充分理解函数曲线的走向，曲线的斜率问题。因此，导数在整个中学阶段是非常重要的，起到连接高等数学与初等数学的作用。

关键词：高中数学；导数；应用

导数是数学中的一个基础概念，也是微积分中的重要概念，它不仅对函数有很重要的解释作用，而且在其他学科比如：物理学、几何学、经济学等等也起着很重要的作用。我们接触过的含有导数的最简单的物理问题就是对瞬时速度的计算，还有计算物质的比热、电流强度、密度等问题，即使它们的物理背景不同，但归根到底都是讨论极限的问题。

导数作为一个数学概念、数学工具，在高中数学中也占有很重要的地位，它涵括了导数的运算法则、基本初等函数的导数公式，对于一些比较抽象的问题，尤其是函数曲线，导数对其切线方程、斜率、曲线的走向形态都做出了很清晰的解释，还有函数的单调性、值域、最值、极值等问题，导数都为大家一一做出了解释。

1、对导数的认识

1.1导数的定义分析

1.1.1导数的背景介绍

导数的思想最初由法国思想家费马（Fermat）为研究极值问题而引入的，但与导数概念直接相联系的这样两个问题：一是已知运动规律求速度，二是已知曲线求它的切线。这是由英国数学家牛顿（Newton）和德国数学家莱布尼茨（Leibniz）分别在研究力学和几何学过程中建立起来的。

在数学界分为数论、代数学、代数几何、拓扑学、数学分析、常微分方程等等，但是在我们上数学课时，老师会告诉我们学习微积分才算学了真正的数学，微积分在数学中占据了非常重要的地位，极大地推动了数学的发展，而微积分又包括积分与微分，在学习的过程中我们会发现，其实对导数进行积分会得到他的原式，所以导数也归为微积分，并且在微积分中地位也是很高的，因此学习导数会帮助我们去学习其他的很多知识，对导数的研究也很有必要。

1.1.2导数的几种定义

导数（Derivative），也叫导函数值，又名微商。当函数y=f（x）的自变量x在一点上产生一个增量时，函数值也会产生一个增量，当在时的极限a如果存在，a即为在处的导数，记作   或。

定义一：设函数y=f(x)在点的某个领域内有定义，若极限              存在，则称函数f在点处可导。并称该极限为函数f在点处的导数，记作

定义二：设函数y=f(x)在点的某个领域内有定义，当自变量x在处变化(x-也在该邻域内)时，也会发生变化；如果   在当时极限存在，则称函数y=f(x)在点处可导，并称这个极限值为函数y=f(x)在点处的导数记为,即导数第二定义

1.2导数的几何意义

导数的几何意义是该函数所代表的曲线在某一点上的切线斜率。一个函数在某一点的导数就是这个函数在这一点附近的变化率，若函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

已知一函数f(x)在x=的切线斜率为k，而斜率k就是该函数在x时的极限，即                      。

由导数的定义可知：k=，所以函数f(x)在（，）处的切线方程为y-=(x-)。而函数曲线的切线与x轴的夹角决定了该曲线斜率的正负，即：设切线与x轴的夹角为，若为锐角，则斜率k为正；若为钝角，则斜率k为负。正如图1-1所表示的那样。 

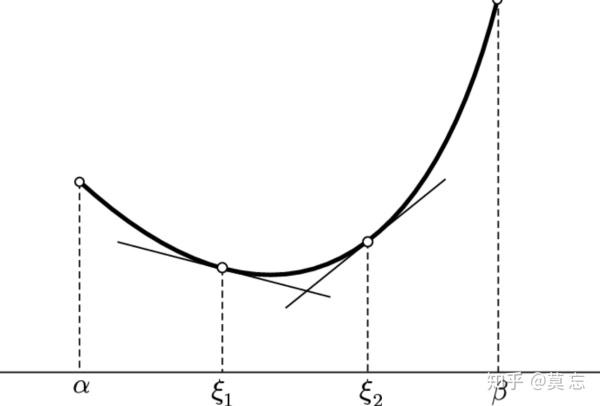
                          图1-1

在高中数学中会提到斜率不存在的知识点，就是当函数曲线的切线与x轴垂直时，即，则 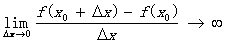        ，所以这时函数的切线斜率不存在。

1.3导数的计算

1.3.1导数的运算法则

                         。

1.3.2基本初等函数的导数公式

虽然已经学过了导数运算法则，我们可以对任何的式子进行求导，但是有一些经常用到的导数，为了方便计算，在数学上就整理了一些基本初等函数的导数公式，如下：

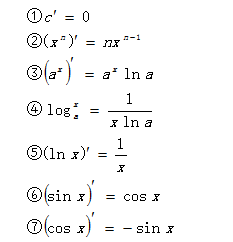
1.3.3复合函数求导

导数在中学数学中涉及的知识点都比较简单，它只是为我们进入大学学习的高等数学（或数学分析）打下基础，让我们更好的理解、认识数学。而在大学我们还学习了复合函数的求导，如下：

为了证明求导函数的求导公式，需要证明一个引理：f在点处可导的充要条件是：在的某邻域U（）内，存在一个点连续的函数H(x),使得，从而【《数学分析》（第三版 上册 高等教育出版社 ）第99页给出证明】。

设u=在点处可导，y=f(u)在点=可导，则复合函数在点可导，且

证：由于f(u)在点可导，由引理必要性部分，存在一个在点连续的函数，使得，且。

又由在点处可导，同理存在一个在点连续的函数，使得，且。

于是就有：

因为在处都可导，u=在处也可导，所以在点处连续。由必要性部分可知在可导。

例一：,求。

解：设，则y=,将看作是跟的复合函数

所以

例二（对数求导法）：设                             求。

分析：看到如此复杂的式子，我们首先想到的是化繁为简，而且该式又是分数的形式，因此运用对数求导法是最简便的计算方法。

解：要先对函数式取对数，得：

再对上面的式子两边分别求导，得：

再对上面的式子做整理，得到最后的答案：

虽然这样的题目也可以用常规的求导方法计算，但是用对数求导法更简便、更好算，在做数学题时我们还是需要对具体问题具体分析，用最适合的方法去解决问题。

2、导数的相关应用

2.1导数在解决函数问题中的应用

2.1.1利用导数判断函数单调性问题

导数是研究函数图像曲线变化率的重要工具之一，是判断函数图像单调性的最好、最常用的方法。

定理：函数在区域上可导，且，若，则函数单调递增；若，则函数单调递减。

运用此方法，既简单又方便，与之前学的定义法求函数的单调性更容易操作又程序化，因此导数思想对于我们来说是很重要的，而且也可以作为函数思想的一个补充，解题时灵活运用，再难的数学问题也可以迎刃而解。

例一：求函数的单调性。

分析：本题主要是探讨导数与函数的单调性的关系，运用导数解决函数的单调性。

解：先对函数进行求导，

接下来判断导函数的正负性。

因为，所以

所以

综上：函数在内单调递增。

2.1.2利用导数求函数的极（最）值问题

导数在研究函数的单调性上发挥着很重要的作用，而且导数对于解决函数的极值、最值问题也有着举足轻重的作用，而函数的最值、极值又与函数的单调性有关系，所以接下来在之前学过的函数的单调性的基础上继续探讨函数的最值、极值问题。

极值是函数在某点附近的一个局部的最大值或最小值，而极值也并不是函数在整个区域内大小的比较。就是说，函数的极大值是该函数在一个特定区域内的最大值，但是在这个函数的整个定义域内不一定是最大值。同理，极小值也是这样。

最值不仅仅存在于函数问题上，在我们的日常生活中也经常出现，在数学应用题上也经常让我们求物体面积、周长等的最大值最小值。函数的最值问题与极值又有着千丝百缕的关系，在我们求闭区间的最值问题时，我们需要运用求极值的方法先求开区间上的极值，然后将端点带进去，把这几个值进行比较，得出最大值与最小值，因此函数的值域问题也随之解决，导数为我们解决这些问题提供了很大的便利。

例一：已知函数                   ，求f(x)的最大值最小值。

分析：该题给出了定义域，上面我们提到要计算闭区间的函数的最值，可以先算开区间的极值，再算出端点值，最后通过比较大小，得出最值。

解：先计算导数值为零时的x值，然后代入函数求出函数值

当           时，，则，，代入函数得到

当时，                  ，x不存在

当           时，函数f的导数为

将              分别代入，

得到；

当时，函数f的导数为             ，

将x=2代入，得到                 ，

因为，所以，函数f(x)的最大值是2，最小值是    。

例二：函数                        的极值是否存在，若存在，求它的极值。

分析：本题我们需要先判断函数对否存在极值，就是研究他的单调性，根据单调性去判断极值是否存在，若存在，就把函数图像的拐点的值带进去，把答案算出来即可。

解：先求导，求函数的单调性与定义域。

，令，得到x=3或x=-1

当时，，函数f(x)单调递增；

当时，，函数f(x)单调递减；

当时，，函数f(x)单调递增；

到这我们可以判断函数存在极值，将x=-1和x=3分别代入,

得到：

综上：f(x)的极小值是-9，极大值是   。

2.1.3用导数求函数曲线的切线方程

在文章开头我们讨论了导数的几何意义，由此可知导数的引入也拓宽了解决几何问题的思路。求函数曲线的切线方程，我们要先知道切线斜率和切点的坐标，因此导数又为此提供了便利。

求函数的切线方程是导数的重要应用之一，用导数的关键在于求出切线方程的切点与斜率k。

已知函数方程，设切点坐标，得到切线方程

有时题目会给出切点坐标，求出斜率即可；有时题目会给出斜率，我们可以运用斜率求出切点坐标，得出切线方程；再就是给出过切线一点的坐标，该点有可能是切点也可能是不是切点，所以要先设出切点坐标，再进行求解。

例：曲线方程，已知一点(2,1)过该曲线的切线，求曲线的切线方程。

解：由于不知道该点是不是切点，所以先设切点，将切点坐标代入曲线方程，得到切点坐标

得到切线方程                        ，将点（2，0）代入，

得到

切线斜率为，所以切线方程为

将斜率与切点坐标代入切线方程，得：，

整理得到

最后得到切线方程：或

2.2导数在研究方程根的分布中的应用

在高中数学必修一中（人教版）学习了零点，零点的定义：若存在一点使得，就称为函数的一个零点。零点定理：函数，如果在上有且连续，则说明在上存在零点。

根据零点的定义，延伸到导数在方程根的应用，将此结论扩展到无穷区间的情形，即：设函数在上连续，且在上保持符号不变，如果与          同号，则说明在上没有实根；如果与           异号，则说明在上有实根。对于在区间的情况，其讨论情况同上。

我们以导数的概念为入口，以导数的应用为核心，运用导数去解决很多疑难问题。

数学是一门逻辑性很强的学科，一环扣一环，一个问题的解决可能要用到很多的知识点，而数学的学习就在于应用，所以我们要加强自己的应用意识，让我们学习的数学有用武之地。

结.论

导数是微积分的一个重要概念，是解决很多问题的有用的工具，它全面体现了数学的价值，既给学生提供了解决问题的方法，又发展了学生许多的数学思想，也给老师为学生讲解数学知识提供了便利。 

中学生要掌握好导数的基本计算方法、初等函数的求导公式以及导数在函数的单调性、极值、最值问题的应用，这对于中学阶段来说是至关重要的，所以有关这方面的题型经常出现在高考最后一个大题。

参考文献

[1]郑柳蓉.导数在高中数学中的应用【J】.《数理化解题研究》，2018（22）:17-18.

[2]李凯.浅析导数在高中数学中的应用【J】.《数码设计》，2017（11）:136-137.

[3]李爱玲.导数在高中数学函数中的应用【J】.《好家长》，2017:138-138.

[4]马丽娜.导数在高中数学中的应用【J】.《数学学习与研究》，2016（20）:146.

  [5]马艳.浅谈导数在高中数学中的应用【J】.《基础教育论坛》，2016（22）:34-36.

[6]胡彬.浅析导数应用中的几种数学思想【J】 .《中学生数理化》，2019(5):20-21.

[7]华东师范大学系编《数学分析》（第三版）上册 北京：高等教育出版社【M】，2001（2013.5重印）.

[8]陈禹.浅析导数在高中数学中的地位与应用[J].课程教育研究,2017(46):1-1.

[9]王焕男.微积分在概率论中的应用[J].科技创新与应用,2019(02):182-184.

[10]刘希团.用导数求切线方程的几种类型[J].考试：高考数学版,2010(9):3-3.

致 谢

毕业论文对于我们这些即将毕业的大学生来说有些困难，从查找文献、搜集相关资料到开始动笔再到现在论文的完成经历了重重困难，我的论文指导老师在我遇到瓶颈的时候给予了我很多的帮助，告诉我应该从哪入手，才使得我拨开云雾见月明，这篇论文才能顺利的写完。

感谢这篇论文所涉及到的各位学者、老师。该篇论文引用了数位学者的研究文献，如果没有各位老师的研究成果，我也就无法完成该篇论文。

由于我的学术研究有限，所以在写该篇论文时会有或多或少的错误，希望各位老师批评指正。

以上就是关于《探究导数在高中数学中的应用》的相关内容，想了解更多毕业论文资讯，敬请关注《山东毕业论文指导网》。如您有论文需求或投稿，欢迎发送邮件至：1624136919@qq.com，也可在下方表单信息中填写您的信息，便可得到专业解答哦！〜(✿◠‿◠✿)〜